Planificación de cultivos como un problema de programación lineal

La planificación de actividades agrarias en una empresa, por medio de modelos de programación lineal puede resumirse en sus rasgos más básicos de la siguiente manera:

El empresario establece el conjunto de cultivos posibles, apoyándose para ello en una serie de variables exógenas a su explotación (suelo, clima, etc.).
A cada cultivo posible se le asocia una cifra representativa de la utilidad que el cultivo representa para el empresario, normalmente se utiliza como indicador de la utilidad el margen bruto de cada cultivo (producto bruto menos gastos variables).
Seguidamente se establecen las variables de decisión x, que representan las superficies dedicadas a cada cultivo en el correspondiente plan.
La función objetivo del programa pretende encontrar el conjunto de valores de las variables de decisión (es decir, el plan de cultivos) que maximiza el margen bruto de la explotación, satisfaciéndose una serie de condiciones. Entre estas restricciones, suelen resultar comunes en la mayor parte de los modelos lineales de planificación de cultivos las siguientes:
- ocupación de la tierra
- frecuencia y sucesión de cultivos
- disponibilidades de mano de obra por períodos
- disponibilidades de capital circulante
- disponibilidades de agua de riego

Un posible esquema de modelo de planificación de cultivos dentro de un enfoque multiobjetivo seria considerar como objetivos a alcanzar los siguientes:

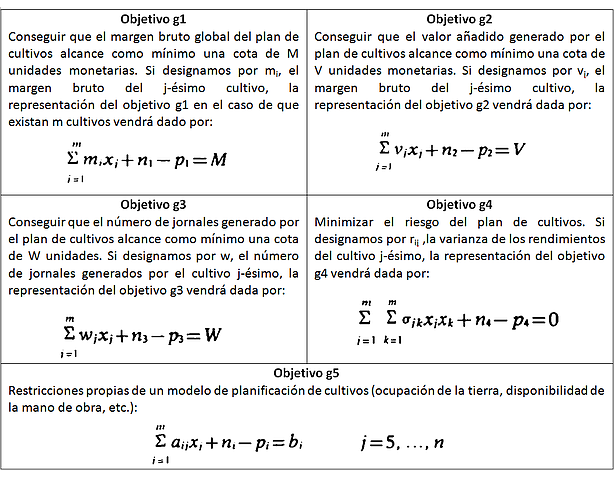
Una vez enunciados y representados los objetivos, pasamos a establecer la estructura de prioridades del modelo.

Como primer paso vamos a suponer que todos los objetivos (restricciones) del grupo g₅ son absolutos, por lo que pasan a formar parte de la prioridad P₁.
La siguiente prioridad en orden de importancia, es decir, la P₂, suponemos que está formada por el objetivo g₃.
La prioridad P₃ la constituyen los objetivos g₁ y g₂, referentes al margen bruto y al valor añadido, considerando el centro decisor que dentro de esa prioridad del objetivo g₂ tiene el doble de importancia que el g₁.
Finalmente, la última prioridad, es decir, la P₄, está formada por el objetivo g₄ referente a la minimización del riesgo del plan de cultivos.

Al existir cuatro niveles de prioridad, la función de logro tendrá cuatro componentes. Dichos componentes, en el supuesto de que las restricciones que conforman el objetivo g₅ y, por tanto, la prioridad P₁ sean todas del tipo menor o igual, serán: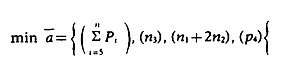

El plan de cultivos óptimo se obtendrá por minimización de la función anterior de forma que se satisfagan en la medida de lo posible los objetivos anteriormente expuestos.

Aplicando el algoritmo de cálculo y la rutina de computador apropiada al programa multiobjetivo anterior se obtendría el plan de cultivos óptimo (x₁*, x₂*,…, x_j*,…, x_m*) que optimiza la función de logro. Supongamos que para la solución óptima la función de logro fuera igual a:

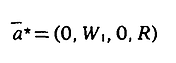La interpretación del vector anterior sería la siguiente:

Los objetivos de la primera prioridad P1 (es decir, las restricciones típicas de los modelos lineales clásicos) se han satisfecho plenamente.
En cuanto al objetivo de la prioridad P2, consistente en conseguir que el plan de cultivos generara W jornales, no se ha podido cubrir en su totalidad.
Los objetivos de la prioridad P₃, referentes a conseguir un plan de cultivos que tuviera un margen global mínimo de M unidades monetarias y un valor añadido global mínimo de V unidades monetarias se ha satisfecho plenamente.
Si se han superado o no los niveles marcados nos los indicarán el valor de las variables de desviación positivas P₁ y P₂.
Si alguna de estas variables toma en el óptimo un valor mayor que cero, este valor nos indicará en cuanto se ha sobre alcanzado el objetivo correspondiente con respecto al nivel mínimo.
Finalmente, en lo referente a la prioridad P₄ que incluye el objetivo de riesgo mínimo, podemos indicar que la varianza de los rendimientos del plan de cultivos óptimo es de R unidades.